终于，终于我们要进入LaTeX最著名的部分了——公式编辑。不得不说，LaTeX对数学公式的处理还是比其他软件高超得多，而我们日常看到的绝大多数排版出来的公式，也都是LaTeX的功劳。LaTeX的数学公式排版功能如此强大，也是由于其关于数学公式方面有一整套完善的框架来完成。下面我们将一点点介绍LaTeX的数学模式。

首先，LaTeX本身自带数学公式的排版指令，但并不是十分丰富和完善。美国数学学会(American Mathematical Society, AMS)为LaTeX提供了一个宏包 amsmath . 这个宏包是我们在进行数学方面写作的时候必须使用的宏包。因此，我们首先需要在导言区写上

 \usepackage{amsmath}

行内公式与行间公式

总得来说，在一篇论文中，公式的表现形式有两种：行内公式与行间公式。行内公式是指与其前后上下文出现在同一行内的公式，而行间公式则是单独为一行的公式。行内公式一般并不是关键性公式，只是个别一个小步骤或者辅助性公式，而行间公式则一般是大型公式或事关键性公式。

说了这么多，行内公式和行间公式有什么区别呢？我们来看一下一个例子：

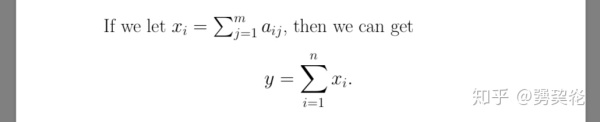
在这个例子中，关于 $\displaystyle x_i$ 的公式是行内公式，而关于 $\displaystyle y$ 的公式是行间公式。而我的源码则是：

If we let $x_i=\sum_{j=1}^ma_{ij}$, then we can get
\[
y=\sum_{i=1}^nx_i.
\]

这里面具体的指令我们之后再说。但我们在这里发现， $...$ 中产生的是行内公式， \[...\] 中产生的是行间公式。对于同样的指令 \sum ，在行内公式里， $\displaystyle j=1$ 和 $\displaystyle m$ 都在它的右边，而在行间公式中，则跑到了它的上面和下面。这也是数学论文写作的规范，也就是，在行内的公式应该压缩其上下，而行间的则不用。这就是行内公式与行间公式的主要区别。

正如上面所说， $...$ 中产生的是行内公式， \[...\] 中产生的是行间公式。而行间公式还有许许多多的环境可以使用，这个之后会提及。那么，怎么在行内产生行间公式的效果呢？用 \displaystyle 命令。也就是， $\displaystyle...$ 其后的行内公式都会有行间公式的效果。比如说，如果我的源码变成了

 If we let $\displaystyle x_i=\sum_{j=1}^ma_{ij}$, then we can get
\[
y=\sum_{i=1}^nx_i.
\]

那么最终排版出来的效果是：

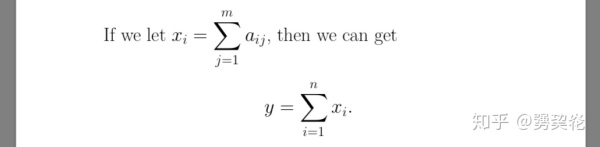
此外，还有针对单个运算符的改变方式，这个会在之后讲到上标与下标的时候提及。

数学模式

根据我们上面的例子，大家应该对LaTeX的数学模式有了一个大致的印象了。也就是说，在正常情况下，是文本模式，基本上就是啥都可以输入，但是不会排版出数学公式来。我如果在正常的文本模式下输入 \sum_{j=1}^n 这样的数学公式的指令，那么是会报错滴。进入数学模式，只有通过 $...$ , \[...\] 或者其他数学模式环境才能进入数学模式。在数学模式中，输入的都会被认作是数学公式。比如说，我如果在数学模式中输入 naive , 排版出来的结果会是 $\displaystyle naive$ . 不仅字体不一样，而且其他文本信息也不一样。因为LaTeX自动会认为这是一个变量的名字。所以，除非特殊情况，否则在绝大多数情况下我们在数学模式中输入的应该只有数学公式。

基础的数学公式

下面，为了大家能尽快使用数学模式，就先给大家介绍一些基础的数学公式的指令。

• 四则运算
  加法 + , 减法 - , 叉乘 \times , 点乘 \cdot , 分数 \frac{}{} , 第一个大括号内为分子，第二个大括号内为分母
• 指数对数
  指数 {}^{} , 第一个大括号内为底数，第二个大括号内为指数；对数 \log_{} , 大括号内为真数；根号 \sqrt{} , 高次根号 \sqrt[]{} , 中括号内为次数
• 上标下标
  上标同指数一样 {}^{} ，下标为 {}_{} .
  这里特别提一句，在有的指令后面， ^ 和 _ 不一定是上下标。比如说 \sum_{}^{} , 在行间公式模式下，就代表正下方和正上方。如果要更改这个方式，可以用 \limits 和 \nolimits 指令。比如说，如果想让行间公式的求和符号的上下标在角上而不在上下方，可以写 \sum\nolimits_{}\nolimits^{} , 如果想让行内公式的求和符号的上下标在上下方而不在角上，可以写 \sum\limits_{}\limits^{} .
• 括号
  如果我们直接输入 ( , ) 这类的括号，那么会被当作一个括号字符，并不会有变化。 我们也可以用 \left( , \right) 这样的命令来产生括号。具体区别是：
  如果我们源码是 (\frac{1}{2}) , 那么排版出来的结果是 $\displaystyle (\frac{1}{2})$ ; 如果我们的源码是 \left(\frac{1}{2}\right) , 那么排版出来的结果是 $\displaystyle \left(\frac{1}{2}\right)$ . 也就是说，括号的大小会跟着里面的内容而变。
  小括号为 \left(...\right) , 中括号为 \left[...\right] , 大括号为 \left\{...\right\} (这里要注意 { 和 } 前均有 \ ), 尖括号为 \left<...\right> , 绝对值为 \left|...\right| , 范数为 \left\|...\right\| .
  此外，还有可能需要我们出现单边括号的情况。比如说 $\displaystyle \left.\frac{x^2}{e^x}\right|_{x=3}$ , 我们只需要将不需要的那半边括号用 \left. 代替即可。比如说刚刚的公式的源码就是 \left.\frac{x^2}{e^x}\right|_{x=3} .
• 求和与求积
  $\displaystyle \sum_{a}^b$ : \sum_{a}^{b} ; $\displaystyle \prod_{a}^{b}$ : \prod_{a}^{b}
• 积分与微分
  $\displaystyle \int_{a}^{b}$ : \int_{a}^{b} ; $\displaystyle \iint_{D}$ : \iint_{D} ; $\displaystyle \iiint_{D}$ : \iiint_{D} ; $\displaystyle \oint_{C}$ : \oint_{C}
  此外，这个内置的积分符号如果觉得有der丑，可以使用宏包 esint , 具体的使用指令可以用texdoc看宏包的说明文档。
  对于微分，有规定说 $\displaystyle \mathrm{d}x$ 中的d一定要是直立体。因此，请在导言区加上一句：
  \def\dif{\mathop{}\!{}\mathrm{d}}
  然后在正文中用 \dif 代替d
  此外，偏微分 $\displaystyle \partial$ : \partial
• 极限
  $\displaystyle \lim_{a\to b}$ : \limit_{a\to b}

此外，还有很多其他的符号，大家在网上都可以方便地找到。

数学环境

接下来，就介绍一些不同的数学环境。

最基础的行间公式环境就是 \[...\] . 这里面的公式默认居中，并且不能换行，没有编号。

如果要添加编号，可以使用 equation 环境，即 \begin{equation}...\end{equation} , 不过该环境依然不能换行

能够换行的环境，最基础的是 gather 环境，即 \begin{gather}...\end{gather} , 换行方式为 \\ 断行。 该环境每行公式均居中，默认编号。其对应的不编号版本为 gather* 环境，即 \begin{gather*}...\end{gather*} . 如果要在某一行不编号，则在该行的 \\ 前加一个 \notag .

其次，可以用 align 环境实现换行且手动对齐。比如说有如下公式：

$\displaystyle \begin{align}f(x)&=\frac{x}{x^2+2x+1}\\&=\frac{1}{x+\frac{1}{x}+2}\end{align}$

它的源码就是

\begin{align}
f(x)&=\frac{x}{x^2+2x+1}\\
&=\frac{1}{x+\frac{1}{x}+2}
\end{align}

也就是说，用 & 来表示对齐。
align 环境是默认编号的，其对应的不编号版本为 align* 环境。

数学模式内的字体

数学模式下，LaTeX使用了不一样的字体。数学模式的字体族可以通过 \setmathfont{} (需要使用 unicode-math 宏包)来设置。

在数学模式下，是默认使用数学字体族的意大利斜体的。如果要使用数学字体族的直立体，可以使用 \mathrm{} 指令，使用数学字体族的粗体，可以使用 \mathbf{} 指令。如果要回到正文字体，可以使用 \text{} 指令。其中， \text{} 指令还可以让我们在数学模式下输入中文，比如说：

$\displaystyle D(x)=\begin{cases}0&x\text{是有理数}\\1&x\text{是无理数}\end{cases}$

的源码就是

D(x)=\begin{cases}
0&x\text{是有理数}
\\1&x\text{是无理数}
\end{cases}