6月21日第一次修改，改正了“排斥或”的错误，增添了一些自然语言的描述。

命题

能判断真假的语句叫做 命题 (proposition)。任何命题都有与之对应的 真值 (truth value) 。

被判断为真的命题叫做 真命题 (true proposition),其真值为1.

被判断为假的命题叫做 假命题 (false proposition),其真值为0.

命题我们一般用小写字母p、q等来表示。

这里我们需要指出的是，无论复杂与否，语句前后是否有明确的逻辑关系，一个完整的句子都可以称作一个命题。

比如说：

“我现在需要个妹子。”是 一个 命题，“我家境不错，仪表堂堂，温文尔雅，博闻强识，现在需要个妹子，并且无论你是男是女，如果你介绍给我好的妹子资源，那么我会感谢你的。”也是 一个 命题。

但是，如果不止一个完整的语句，比如说“你有妹子。我没有妹子。”就不是一个命题。

从某种意义上，一个没有句号，而是逗号的可以判断真假的句子就是一个命题（当然每个分句之间，必须有逻辑联结词，请看下文）。

命题之间的关系

到目前为止，可以和命题连接的符号只有冒号，也就是，命题p：我需要妹子。那么接下来，我们要给出其他的可以和命题连接的符号。同时，也阐明了任意两个命题的关系。

如果命题p能推出命题q，那么称命题p为命题q的 充分条件 (sufficient condition),命题q为命题p的 必要条件 (necessary condition),记作 $\displaystyle p\Rightarrow q$ 或 $\displaystyle q\Leftarrow p$ .如果命题p既是命题q的充分条件也是命题q的必要条件，那么p和q互为 充要条件 ，p和q等价，记作 $\displaystyle p\Leftrightarrow q$ 。

逻辑联结词

接下来，我们引入 逻辑联结词 的概念。

首先，引入这个概念有两个原因：一是为了更方便地判断一个复杂命题的真假性，请见下面真值表；二是通过引入逻辑联结词，我们便可以引入对命题的运算，使命题不再孤立。

一阶逻辑联结词（即只对一个命题的运算）： 非 （NOT）

我们定义一个命题p的 否定 (negation)（这里要和后面的否命题相区别） $\displaystyle \neg p$ 为与原命题真假性相反的命题，读作非p。

比如，“我现在需要妹子”的否定是“我现在不需要妹子”，“你不可能写错”的否定是“你可能写错”。

一般来说，就是 一个命题和其否定必定有一个会是真的，一个会是假的。

特别需要指出的是，p是一个命题， $\displaystyle \neg p$ 也是一个命题。

二阶逻辑联结词（即对两个命题的运算）：且（AND）、或（OR）、如果……那么……、……当且仅当……

我们定义两个命题p和q的 合取 (conjunction) $\displaystyle p\wedge q$ ,当且仅当p和q均为真时， $\displaystyle p\wedge q$ 为真，读作p且q。比如命题“我很帅且需要妹子。”，如果我不帅或者我不需要妹子，那么这个命题就是假的，只有我帅而且也需要妹子，这个命题才是真的。

我们定义两个命题p和q的 析取 (disjunction) $\displaystyle p\vee q$ ,当且仅当p和q均为假时， $\displaystyle p\wedge q$ 为假，读作p或q。

这里需要指出，这里的“或”和我们口语中的“或”有一定的差异。

下面是我们口语中的一句话：“你可以六点或七点再来。”

这实际是我们在逻辑中所称的“ 排斥或 ” (exclusive disjunction)，即或的前后两件事只能有一件事发生，用逻辑的语言写出来实际是 $\displaystyle (p\wedge \neg q)\vee (\neg p\wedge q)$ 。

而逻辑中的或，在口语中会以“我爱唱歌或爱跳舞。”的形式出现，我可以既爱唱歌也爱跳舞，也可以只爱唱歌和跳舞中的一种。

我们定义两个命题p和q的 蕴涵式 (implication) $\displaystyle p\rightarrow q$ ，它的真假性等价于 $\displaystyle \neg p\vee q$ 。即，如果p为假，那么无论q真假与否， $\displaystyle p\rightarrow q$ 均为真；如果p为真，那么q为真时， $\displaystyle p\rightarrow q$ 方为真。 $\displaystyle p\rightarrow q$ 读作如果p，那么q。

其实这个定义是可以理解的，比如“如果你能找到女朋友，那么我就去抄《数分》。”无论我会不会去抄《数分》，我说这句话的潜台词是你一定找不到女朋友，所以这句话就是真的，我不能算说谎。

我们定义两个命题p和q的 等价式 (equality) $\displaystyle p\leftrightarrow q$ ，当且仅当p和q真假性相同时， $\displaystyle p\leftrightarrow q$ 为真（这也就是说，即使p和q都是假的， $\displaystyle p\leftrightarrow q$ 也是真的）。 $\displaystyle p\leftrightarrow q$ 读作p，当且仅当q。

关于蕴涵式和等价式，我们还需要知道，即使这式子为真，构成这式子的两个命题也不一定要有逻辑关系。比如说，命题： $\displaystyle \left( x^2\geq 0 \right) \rightarrow \left( 5 \mod3=2 \right) $ 也是一个真命题。

这里有一点需要阐明，两个命题的蕴涵式和等价式和我们之前讲的充分条件和充要条件不完全相同，前者是构成一个命题的方式，后者是两个命题之间的关系。想详细了解区别的请去搜索“ 元语言 (metalanguage)”,这里不再赘述。不过事实上，若 $\displaystyle p\rightarrow q$ 为真，则 $\displaystyle p\Rightarrow q$ ;若 $\displaystyle p\leftrightarrow q$ 为真，则 $\displaystyle p\Leftrightarrow q$ 。

以上便是五种逻辑联结词：非、且、或、如果……那么……、……当且仅当……。

有一个小窍门记住且、或的符号：

下面介绍 真值表 (truth table):

对于一个复杂的命题，比如 $\displaystyle \left( x>0 \right)\vee \left(( x\in R)\rightarrow (x\in C) \right) $ ,或者 $\displaystyle (p\vee \neg q)\wedge \left( r\rightarrow q \right) $ ,我们判断其真假性时较为麻烦，所以我们可以使用真值表。如下：

由真值表可知，只有p真q假r真或p假q假r真或p假q假r假时该命题为假。

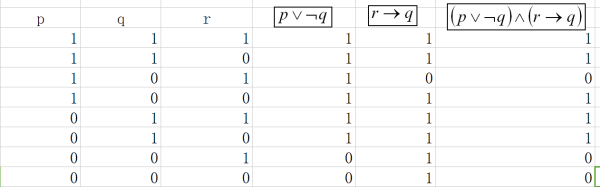
真值表是证明逻辑等价式的最基本方式

逻辑量词

同时，我们还有两种逻辑量词：对于任意(for all)、存在(there exists)

我们定义 全称量词 (universal quantifier) $\displaystyle \forall $ ，它代表接下来的命题对于所有我们讨论范围内的元素都为真。严格的格式为 $\displaystyle \forall x\left(p(x)\right)$ ,其中 $\displaystyle p(x)$ 是关于x的命题，称为该全称量词的 辖域 (scope)。

比如： $\displaystyle \forall x\left( \left(\left( x>0 \right)\wedge \left( x \in R\right) \right) \rightarrow \left( x^{2}>0 \right) \right)$ 是一个合法的写法,该全称量词的辖域为 $\displaystyle \left(\left( x>0 \right)\wedge \left( x \in R\right) \right) \rightarrow \left( x^{2}>0 \right) $ 。

我们生活中也常用全称量词表述观点，比如说“在座的各位都是辣鸡。”我不是针对某个人，而是指在座的各位，所以是对我们讨论范围内的所有元素，都是辣鸡。

我们定义 特称量词 (existential quantifier) $\displaystyle \exists $ ，它代表接下来的命题对于我们讨论范围内的至少一个元素为真。严格的格式为 $\displaystyle \exists x(p(x))$ ,其中 $\displaystyle p(x)$ 是关于x的命题，称为该特称量词的辖域。

口语中我们运用特称量词的例子有“我们中出了个叛徒。”我们中至少出了一个，而非我们都是，叛徒，这是我们讨论范围内至少有一个元素符合我们的命题。

但是，我们高中学的量词格式，不是一般是“ $\displaystyle \forall x>0,x^2>0$ ”这种么？

实际上，这是一种简化的写法，用在不是专门讨论逻辑的地方。那么这种写法对应的标准格式是什么呢？

我们知道，" $\displaystyle \forall x>0,x^2>0$ "和" $\displaystyle \forall x^2>0,x>0$ "并不是等价的命题，那么我们上面介绍的四种二阶逻辑联结词中，哪一个是类似这样非对称的呢？只有一个——蕴涵式。事实上，这种全称量词的写法“ $\displaystyle \forall p(x),q(x)$ ”正是标准的写法" $\displaystyle \forall x\left( p(x)\rightarrow q(x) \right) $ "的简写。

相反地，" $\displaystyle \exists x>0,x^2>0$ "却是和" $\displaystyle \exists x^2>0,x>0$ "等价的，表述的是同一件事情。即存在 x ，使这两件事是同时成立。事实上，这种特称量词的写法" $\displaystyle \exists p(x),q(x)$ "(在某些书上，会写成" $\displaystyle \exists p(x),s.t.q(x)$ ","s.t."是"such that"的简写)的标准写法正是 $\displaystyle \exists x\left( p(x)\wedge q(x) \right) $

逻辑恒等式

下面给出一些逻辑恒等式，证明的话直接用真值表即可。

$\displaystyle \left( p\vee (q\wedge r) \right) \Leftrightarrow \left( (p\vee q)\wedge (p\vee r) \right) $ , $\displaystyle \left( p\wedge (q\vee r) \right) \Leftrightarrow \left( (p\wedge q)\vee (p\wedge r) \right) $

$\displaystyle (\neg \left( p\vee q \right) )\Leftrightarrow (\neg p\wedge \neg q)$ , $\displaystyle (\neg \left( p\wedge q \right) )\Leftrightarrow (\neg p\vee \neg q)$

$\displaystyle \neg \neg p\Leftrightarrow p$

接下来便是我觉得逻辑学对大学数学最重要的两条：

$\displaystyle \left( \neg \left( \forall x\left( p(x) \right) \right) \right) \Leftrightarrow\exists x\left( \neg p(x) \right) $ , $\displaystyle \left( \neg \left( \exists x\left( p(x) \right) \right) \right) \Leftrightarrow\forall x\left( \neg p(x) \right) $

从某种意义上讲，这就是反证法的原理。有时候有一些含有全称量词的命题我们搞不清楚，就可以考虑它的否定，只要它否定为假，那么它自身就为真。

这个虽然逻辑语言表述很复杂，但实际上非常好理解，比如说，命题“你出差的每一晚，我都一个人在想你。”的否定就是“有一个你出差不在的晚上，我没有一个人在想你。”

根据我们上面的规则，有 $\displaystyle \neg \forall x\left( p(x)\rightarrow q(x) \right) \Leftrightarrow \exists x\left( p(x)\wedge \neg q(x) \right) $ 。或者写成：

$\displaystyle \neg \forall p(x),q(x)\Leftrightarrow \exists p(x),s.t.\neg q(x)$

在高等数学中，我们会遇到许多含有多种量词的命题，比如说(Cauchy收敛准则):

$\displaystyle \forall \varepsilon >0,\exists N=N(\varepsilon),s.t.\forall (n>N)\wedge (m>N),\left| a_n-a_m \right| <\varepsilon $

它的否定就是：

$\displaystyle \exists \varepsilon >0,s.t.\forall N=N(\varepsilon),\exists (n>N)\wedge (m>N),s.t.\left| a_n-a_m \right| \geq \varepsilon $

那么对于第二个命题来说，m和n究竟是固定的数，还是随N而变的数呢？这就需要我们注意到几个量词的顺序。

我们来看以下两个命题:

$\displaystyle \forall x>0,\exists y\in R,s.t.y>x$
$\displaystyle \exists y\in R,s.t.\forall x>0,y>x$

由于第一个命题中特称量词在全称量词的辖域内，故y是可以随x改变的；而第二个命题中，特称量词在全称量词的辖域外，故y是不可以随x改变的。对于这两个命题的证明（伪）都很简单：

第一个命题中， $\displaystyle \forall x>0$ ,取y=x+1，则y>x成立。

第二个命题中，我们证其否定为真即可。而且否定为: $\displaystyle \forall y\in R,\exists x>0,s.t.y\leq x$ 。故取x=|y|+1即可。

举个现实生活中的例子，命题“我生命中每一个阶段，都有一个女性在等着我。”和“有一个女性，在我生命中的每一个阶段都等着我。”是完全不一样的两个命题，前者的女性可以随着我生命的阶段的变化而变化，而后者只能有一个女性。

逆命题、否命题、逆否命题

接下来再介绍一些特殊的命题关系：逆命题、否命题、逆否命题。

对于 蕴涵式 命题 $\displaystyle p\rightarrow q$ ,称命题 $\displaystyle q\rightarrow p$ 与其互为 逆命题 (converse)， $\displaystyle \neg p\rightarrow \neg q$ 与其互为 否命题 (inverse)， $\displaystyle \neg q\rightarrow \neg p$ 与其互为 逆否命题 (contrapositive)。特别地，如果该蕴涵式命题是一个量词的辖域，那么其逆命题、否命题、逆否命题中的量词不变。如” $\displaystyle \forall x>0,x^2>0$ ”的逆命题为" $\displaystyle \forall x^2>0,x>0$ “

由于 $\displaystyle (\neg q\rightarrow \neg p)\Leftrightarrow (q\vee \neg p)\Leftrightarrow (p\rightarrow q)$ ,故 一个命题的逆否命题与其真假性相同 。

举个大家都很熟悉的例子，“如果有一个人是我，那么这个人爱你”的逆否命题是“如果有一个人不爱你，那么这个人不是我。”

而很显然，一个命题的逆命题与否命题和其真假性无必然关系。（这点便可以很容易区别一个命题的否命题和一个命题的否定）

推理系统

最后介绍一些推理系统的知识：

我们生活中运用到的推理系统，称为公理推理系统，它包含非空的字母表、合式公式集、公理集、推理规则集。这些高端的名词，总的来说，就是我们上面讲的各种逻辑符号及规则，加上公理。

公理 (axiom)为该逻辑系统中所有证明的源头，是一些互为既不充分也不必要命题且互不矛盾的命题。在这个推理系统中，我们认为所有的公理都恒为真命题。

定理 (theorem)为非公理的真命题，由一个或多个公理推出。

定理有时又可分为 引理 (lemma)、 推论 (corollary)，但这已和逻辑无大关系了.

最后的最后……

由于知识欠缺，我的介绍有许多欠缺、错误，希望大家积极指正、补充~

给大家卖个萌（划）鞠个躬！