在这样一个正经专栏《面向高中毕业生的数学介绍》中出现这样一个诡异名字的文章，大家会不会觉得有些诧异呢。

好吧我起这个名字就是故意的。

数学中确实存在基

我们今天要讲的基，不是Newton与Leibniz,也不是Abel与Galois

而是 滤子基 （Filter base），简称 基 (base).

引入基的想法很朴实，在数学家们处理函数极限的过程中，产生了许多定理。由于函数极限可以是 $\displaystyle \lim_{x \rightarrow x_0}$ 、 $\displaystyle \lim_{x \rightarrow +\infty}$ 、 $\displaystyle \lim_{x \rightarrow -\infty}$ 、 $\displaystyle \lim_{x \rightarrow \infty}$ 这四种情形，但在许多定理中，这四种情形都适用，数学家就不得不把同一个定理写四遍，或者在每条定理的后面写一句“在极限趋于无穷时亦然。”这无形之中就给数学家增添了许多不必要的麻烦。

为了解决这个问题，数学家就想搞一个记号，能代替所有的极限情形。这不搞不要紧，一搞啊，就弄了个基出来。

滤子基：

由集合X的某些子集 $\displaystyle B \subset X$ 组成的集族 $\displaystyle \bf { B}$ 称为集合X的基，如果它满足以下两个条件：
1. $\displaystyle \forall B \in {\bf B} ,B \neq \emptyset$
2. $\displaystyle \forall B_1 \in {\bf B},\forall B_2 \in {\bf B},\exists B \in {\bf B},s.t.B \subset B_1 \cap B_2$

基上的极限：

设 $\displaystyle X \rightarrow R$ 的函数 $\displaystyle y=f(x)$ , $\displaystyle \bf B$ 是X上的一个基。如果对于点 $\displaystyle a \in R$ 的任何邻域 $\displaystyle N(a)$ ,存在基 $\displaystyle \bf B$ 的元素 $\displaystyle B \in \bf B$ ,使 B 的像 $\displaystyle f(B)$ 包含在 $\displaystyle N(a)$ 中，就说 a 是函数 $\displaystyle y=f(x)$ 关于基 $\displaystyle \bf B$ 的极限。记作 $\displaystyle \lim_{\bf B}f(x)=a$ .

四种R上的极限的基：

$\displaystyle x \rightarrow x_0$ ： $\displaystyle {\bf B}=\{B|B=\{x|0<|x-x_0|<\delta\},\delta \in R^+\}$
$\displaystyle x \rightarrow +\infty$ ： $\displaystyle {\bf B}=\{B|B=\{x|x>M\},M\in R \}$
$\displaystyle x \rightarrow - \infty$ ： $\displaystyle {\bf B}=\{B|B=\{x|x<M\},M\in R \}$
$\displaystyle x \rightarrow \infty$ ： $\displaystyle {\bf B}=\{B|B=\{x||x|>M\},M\in R \}$

哇，不是想简化我们的叙述嘛，怎么又搞出了这么个劳什子出来！

本宝宝当初看了快一个礼拜才看懂这是个什么……

宝宝心里苦，但宝宝不说。

用通俗的语言来讲，基呢，是这么个东西：

首先，它是集族——集合的集合，也就是说，它的元素是一些集合。其次，它的元素中没有空集。接着，它的任意两个元素之交也含有这个集族中的元素。由于空集不属于这个集族，所以综合二三两点，得出该集族的任意两个元素的交集非空。这么曲折的定义是为了后面讲基上的极限。

为了说明基上的极限，我们不妨拿自变量趋于常数的极限来作例子。

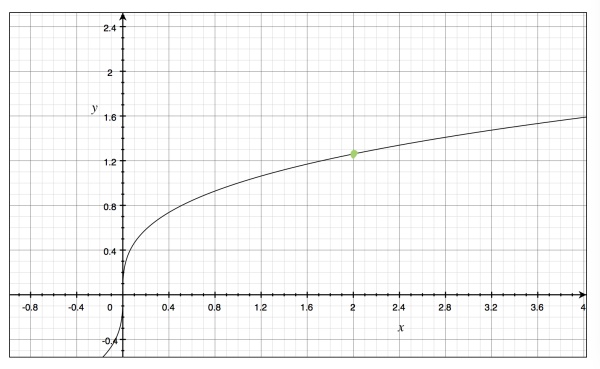
这是函数 $\displaystyle f(x)=\sqrt[3]{x}$ 的图像。我想以此来说明基上极限的定义。我取一个点，比如说 $\displaystyle (2,\sqrt[3]{2})$ .取 $\displaystyle {\bf B}=\{B|B=\{x|0<|x-2|<\delta\},\delta \in R^+\}$ 为基，那为什么 $\displaystyle \lim_{\bf B}f(x)=\sqrt[3]2$ 呢？

为了说明这个，我们需要阐释两点：

1. $\displaystyle \sqrt[3]2$ 确实是这个基上的极限

2.不是 $\displaystyle \sqrt[3]2$ 的数都不是这个基上的极限

第一点：

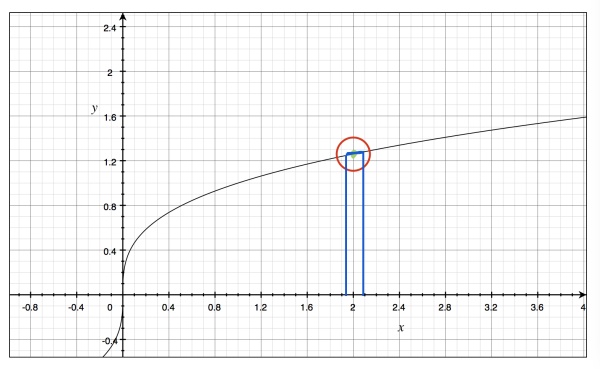
按照我们对基上极限的定义，我们对这个点的任意邻域进行图上的操作。那个蓝框框对应的x轴部分就是我们可以从基 $\displaystyle \bf B$ 中取的那个元素。

第二点：

对于不是 $\displaystyle \sqrt[3]2$ 的数，不妨是比它大一点点的一个数，那么我们就像图中一样，先做一条黄色的线，黄色线以下的部分取蓝框框，那么蓝框框对应的x轴部分是我们取的基 $\displaystyle \bf B$ 中，像不在其邻域里的元素

通过以上两点的分析，我们确实得出了这个基的极限的意义。

事实上，这也是一个普适性的定义，不依赖于实数集。对于更高层次的函数极限，我们之前讲的已经不再适用，但这个却始终可以作为函数极限的定义。

对于我们初学者来说，我认为对于基的定义，我们了解即可，它是为了更高层次做准备的。我们需要掌握的，是四种极限的对应的基，和基上极限的定义。那么，究竟为什么把基定义成集合的集合呢？从某种意义上，根据我们前面对基的极限的阐释，可以发现我们一直在找一些 $\displaystyle x_0$ 的邻域，但我们找的邻域可能多种多样，把所有这样的邻域放在同一个集合里，那么就是一件很顺理成章的事。

那么为什么用基，就可以把四种极限简化成一种呢？实际上，这用了一个障眼法。它只不过对四种极限定义了各自的基，用同样的记号表示出来而已。但是这样写，确实更加科学，也更加简洁。